Declaration
template <class InputIterator1, class InputIterator2, class T>
T inner_product(InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2, T init);
template <class InputIterator1, class InputIterator2, class T,
class BinaryOperation1, class BinaryOperation2>
T inner_product(InputIterator1 first1, InputIterator1 last1,
InputIterator2 first2, T init, BinaryOperation1 binary_op1,
BinaryOperation2 binary_op2);
Description
For the sequence 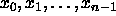 in the range
[ first1, last1)
, and the sequence
in the range
[ first1, last1)
, and the sequence 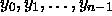 in the range beginning at first2
, the first
inner_product function returns
in the range beginning at first2
, the first
inner_product function returns

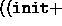
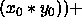
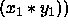
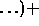
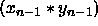 ,
and the second inner_product
function returns
,
and the second inner_product
function returns 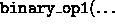
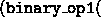
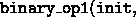
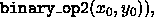
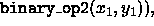

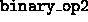
 .
The first function may be used to calculate the
sum-of-products
of the elements in two sequence, and the second function may be used more
generally to compute the inner
product
of the elements of two sequences using two binary functions (these may be the
same function).
.
The first function may be used to calculate the
sum-of-products
of the elements in two sequence, and the second function may be used more
generally to compute the inner
product
of the elements of two sequences using two binary functions (these may be the
same function).
If the product-of-sums is desired, the second function may be used with a function object that returns the sum of the contents of two iterators passed for the binary_op2 parameter and a function object that returns the product of an object of type T and an object of the return type of binary_op2 passed for the binary_op1 parameter.
Type requirements
Group Generalized numeric operations.
Time complexity Linear.
The number of applications of operator+ or the function object binary_op1, and the number of applications of operator* or the function object binary_op2, is n, where n is the size of the range [ first1, last1) , each.
Space complexity Constant.
Mutative? No.
Details Returns init if first1 = last1. Assumes that binary_op1 and binary_op2 do not cause side effects .
Glossary terms BinaryOperation, constant space, dereference type, function object, function object type, inner product, InputIterator, iterator, linear time, mutative, operator+, operator*, range, sequence, side effect.
Example Select here to view the source code for the example.
Implementation Select here to view source code (Copyright (C) 1994, Hewlett-Packard Company) for this algorithm.
Implementation notes The inner product is calculated by adding (or performing the first specified binary operation) the product (or the second specified binary operation) of each pair of values, in order, to the initial value to create a modified initial value.