Find the first match of a subsequence with a sequence

Source code

Declaration

template <class ForwardIterator1, class ForwardIterator2>
inline ForwardIterator1 search(ForwardIterator1 first1, ForwardIterator1 last1,
                               ForwardIterator2 first2, ForwardIterator2 last2);

template <class ForwardIterator1, class ForwardIterator2,
          class BinaryPredicate>
inline ForwardIterator1 search(ForwardIterator1 first1, ForwardIterator1 last1,
                               ForwardIterator2 first2, ForwardIterator2 last2,
                               BinaryPredicate binary_pred);

Description            For the sequ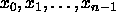ence in the range [ first1, last1) and the sequence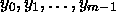

in the range [ first2, last2) , each search  function returns an iterator i referring to the first element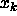

such that 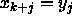for 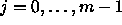or last1 if no such subrange  occurs. In the first function checks for element equality are made with operator!=, while in the second they are made with the function object binary_pred.

Type requirements

• ForwardIterator1 and ForwardIterator2 must be at least regular forward iterators .
• BinaryPredicate must be a function object type that provides int operator()(T1, T2), where T1 and T2 are the dereference types of ForwardIterator1 and ForwardIterator2, respectively.

Group Non-mutating sequence operations.

Time complexity Quadratic.

In the worst case the number of applications of operator!= or binary_pred is 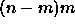, which is 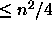(if m > n , the number is 0).

Space complexity Constant.

Mutative? No.

Details These functions generalize the usual notion of matching of strings      (sequences of characters) to sequences over any type.

Glossary terms BinaryPredicate, constant space, dereference type, ForwardIterator, function object, function object type, iterator, Knuth-Morris-Pratt algorithm, linear time, mutative, operator !=, predicate, quadratic time, range, sequence, string, subrange, subsequence, worst-case behavior.

Example Select here to view the source code for the example.

Implementation Select here to view source code (Copyright (C) 1994, Hewlett-Packard Company) for this algorithm.

Implementation notes The Knuth-Morris-Pratt algorithm  is not used here. While the KMP algorithm  guarantees linear time, it tends to be slower in most practical cases than the naive algorithm with worst-case quadratic behavior. The worst case is extremely unlikely.